Definición: La hipérbola como lugar geométrico está formada por el lugar geométrico de los
puntos del plano cuya diferencia de distancias a dos puntos fijos llamado
focos, y que llamaremos F y F', es constante. Es decir,
P es un punto de la hipérbola si y sólo si PF-PF' es constante, P es un punto de la hipérbola si y sólo si
PF'-PF es constante. Estas dos
condiciones se pueden resumir en una: P es un punto de la hipérbola si y sólo
si |PF-PF'| es una cantidad constante.
Elementos de la Parábola
Focos:
Son los puntos fijos F y F'.
Eje focal : Es
la recta que pasa por los focos.
Eje secundario o imaginario:
Es la mediatriz del segmento .
Centro: Es
el punto de intersección de los
ejes.
Vértices
: Los puntos A y A' son los puntos de
intersección de la hipérbola con el eje focal.
Los puntos B y B' se obtienen como
intersección del eje imaginario con la circunferencia que tiene por centro uno
de los vértices y de radio c.
Radios vectores: Son
los segmentos que van desde un
punto de la hipérbola a los focos: PF y PF'.
Distancia focal: Es el
segmento FF’de longitud
2c.
Eje mayor: Es el
segmento AA’ de longitud 2a.
Eje menor: Es el
segmento BB’ de
longitud 2b.
Ejes de simetría: Son
las rectas que contienen al eje
real o al eje imaginario.
Asíntotas: Son
las rectas de ecuaciones: y= --
bx/a
; y = bx/a
Relación entre los semiejes: C2= a2 + b2
La excentricidad: La
excentricidad mide la abertura
mayor o menor de las ramas de la hipérbola.
e
= c/a c ≥
a e ≥ 1
Ecuaciones
Analíticas de la Hipérbola
caso
1. Hipérbola con focos F’(-c, 0) y F(c, 0) ; c > 0.
TEOREMA:
la
ecuación de la hipérbola centrada en el origen y cuyos focos están en los
puntos F(-c, 0) y F(c, 0) viene dada por:
Caso
2.
Hipérbola
con focos en F’(0, -c) y F(0, c) ; c >
0.
TEOREMA:
La ecuación de la hipérbola
centrada en el origen y cuyos focos están en los puntos F’(0, -c) y F(0, c) viene dada por: b2 = c2 - a2
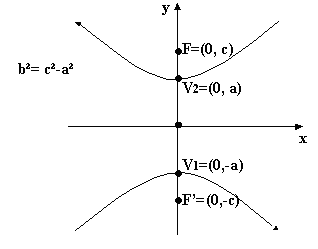
No hay comentarios:
Publicar un comentario